Polynomial equations an interesting subject in theory of numbers, occupy a pivotal role in the realm of mathematics and have a wealth of historical significance. The theoretical importance of polynomial equations of third degree in two unknowns having integral coefficients is great as they are closely connected with many problems of number theory. Specifically, the third degree polynomial equations having two unknowns in connection with elliptic curves occupy a pivotal role in the region of mathematics. This paper discusses on finding many solutions in integers to a typical third degree equation having two variables expressed as a(x-y)3=8bxy. The substitution strategy is employed in obtaining successfully different choices of solutions in integers. Some of the special fascinating numbers, namely, Pyramidal numbers, Polygonal numbers, Centered pyramidal numbers, Centered polygonal numbers, Thabit ibn Qurra numbers, Star numbers, Mersenne numbers and Nasty numbers (numbers expressed as product of two numbers in two different ways such that the sum of the factors in one set equals to the difference of factors in another set) are discussed in properties. These special numbers are unique. and have attractive characterization that set them apart from other numbers. The process of formulating second order Ramanujan numbers with base numbers as real integers is illustrated through examples.
| Published in | Pure and Applied Mathematics Journal (Volume 13, Issue 2) |
| DOI | 10.11648/j.pamj.20241302.12 |
| Page(s) | 29-35 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Non-Homogeneous Cubic, Binary Cubic, Integer Solutions, Ramanujan Numbers
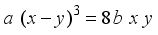 . Substitution strategy is employed in obtaining successfully different choices of integral points to the above non-homogeneous third degree equation having two variables. The process of formulating second order Ramanujan numbers with base numbers as real integers is illustrated through examples.
. Substitution strategy is employed in obtaining successfully different choices of integral points to the above non-homogeneous third degree equation having two variables. The process of formulating second order Ramanujan numbers with base numbers as real integers is illustrated through examples. 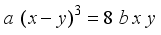 (1)
(1) 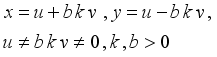 (2)
(2) 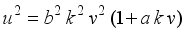 (3)
(3) 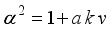 (4)
(4) 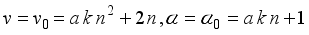 (5)
(5) 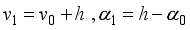 (6)
(6) 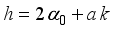
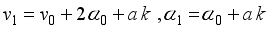
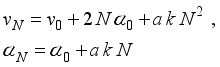 (7)
(7) 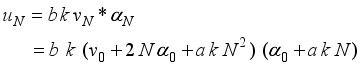 (8)
(8) 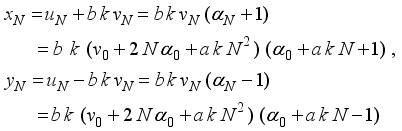 (9)
(9) 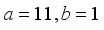
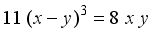 (10)
(10) 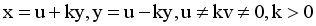 (11)
(11) 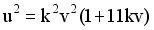 (12)
(12) 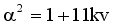 (13)
(13) 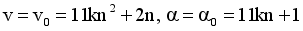 (14)
(14) 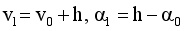 (15)
(15) 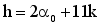
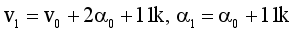
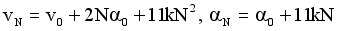 (16)
(16) 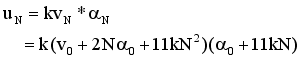 (17)
(17) 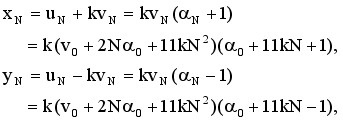 (18)
(18) 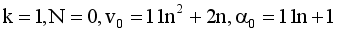
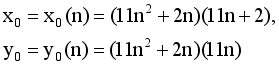 (19)
(19) n | X0(n) | y0(n) |
|---|---|---|
1 | 132 | 11*13 |
2 | 2*242 | 44*24 |
3 | 3*352 | 99*35 |
4 | 4*462 | 176*46 |
5 | 5*572 | 275*57 |
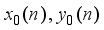 are alternatively odd and even.
are alternatively odd and even. 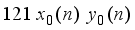 is a cubical integer
is a cubical integer 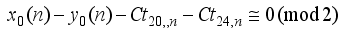
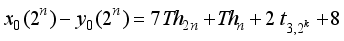
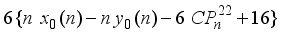 is a nasty number
is a nasty number 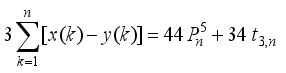
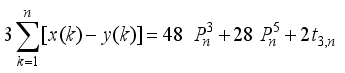
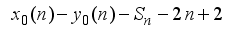 is a perfect square
is a perfect square 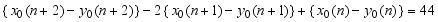
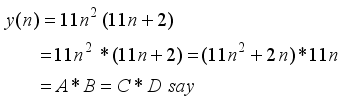
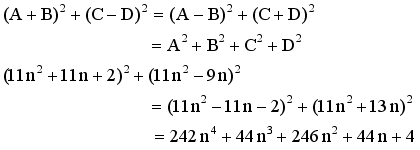
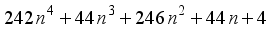
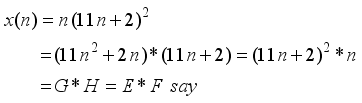
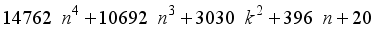
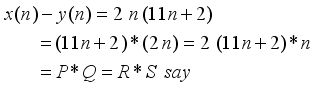
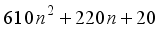
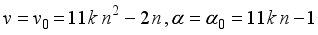
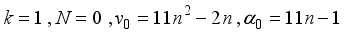
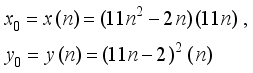
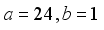
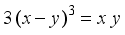 (20)
(20) 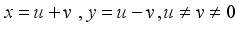 (21)
(21) 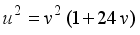 (22)
(22) 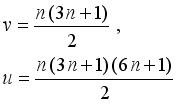 (23)
(23) 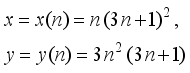 (24)
(24) n | x(n) | y(n) |
|---|---|---|
1 | 16 | 12 |
2 | 98 | 84 |
3 | 300 | 270 |
4 | 676 | 624 |
5 | 1280 | 1200 |
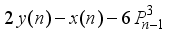 is a cubical integer
is a cubical integer 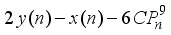 is a multiple of 2
is a multiple of 2 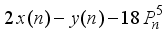 is a multiple of 2
is a multiple of 2 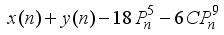 is a multiple of 4
is a multiple of 4 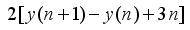 represents the area of Pythagorean triangle
represents the area of Pythagorean triangle 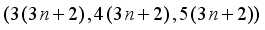
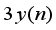 is a perfect square for
is a perfect square for 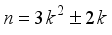
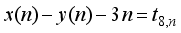
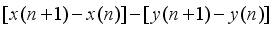 is a perfect square for
is a perfect square for 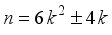
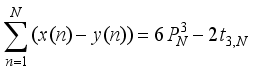
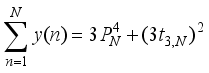
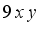 is a cubical integer
is a cubical integer 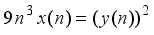
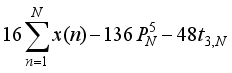 is written as the difference of two squares
is written as the difference of two squares 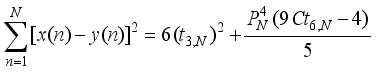
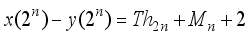
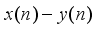 is a perfect square when
is a perfect square when 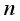 takes the values
takes the values 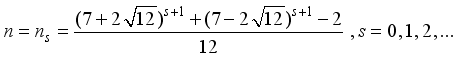
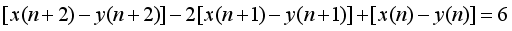
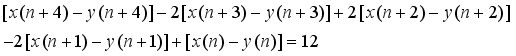
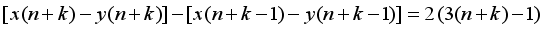
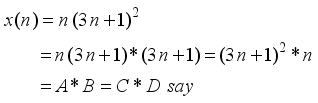
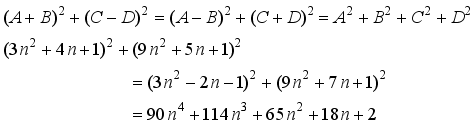
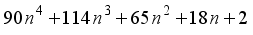 represents the second order Ramanujan number.
represents the second order Ramanujan number. 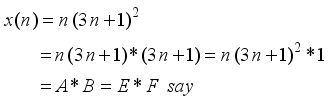
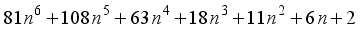
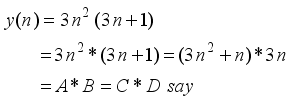
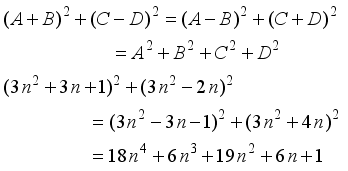
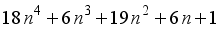 represents the second order Ramanujan number.
represents the second order Ramanujan number. 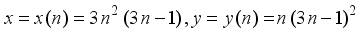
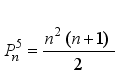
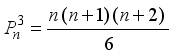
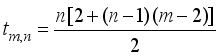
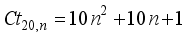
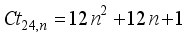
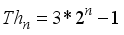
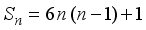
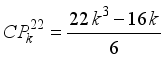
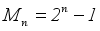
| [1] | L. E. Dickson, History of Theory of Numbers, Vol. 2, Chelsea Publishing Company, NewYork, 1952. |
| [2] | L. J. Mordell, Diophantine equations, Academic press, New York, 1969. |
| [3] | M. A. Gopalan, G. Sangeetha, “On the ternary cubic Diophantine equation y2=Dx2+z3”, Archimedes J. Math 1(1), 2011, 7-14. |
| [4] | M. A. Gopalan, B. Sivakami, “Integral solutions of the ternary cubic equation 4x2-4xy+6y2=((k+1)2+5)w3”, Impact J. Sci. Tech, 6(1), 2012, 15-22. |
| [5] | M. A. Gopalan, B. Sivakami, “On the ternary cubic Diophantine equation 2xz=y2(x+z)”, Bessel J. Math, 2(3), 2012, 171-177. |
| [6] | M. A. Gopalan, K. Geetha, “On the ternary cubic Diophantine equation x2+y2-xy=z3”, Bessel J. Math., 3(2), 2013, 119-123. |
| [7] | M. A. Gopalan, S. Vidhyalakshmi, A. Kavitha “Observations on the ternary cubic equation x2+y2+xy=12z3”, Antartica J. Math, 10(5), 2013, 453-460. |
| [8] | M. A. Gopalan, S. Vidhyalakshmi, K. Lakshmi, “Lattice points on the non-homogeneous cubic equation x3+y3+z3+(x+y+z)=0”, Impact J. Sci. Tech, 7(1), 2013, 21-25. |
| [9] | M. A. Gopalan, S. Vidhyalakshmi, K. Lakshmi “Lattice points on the non-homogeneous cubic equation x3+y3+z3-(x+y+z)=0”, Impact J. Sci. Tech, 7(1), 2013, 51-55. |
| [10] | M. A. Gopalan, S. Vidhyalakshmi, S. Mallika, “On the ternary non-homogenous cubic equation x3+y3-3(x+y)=2(3k2-2)z3”, Impact J. Sci. Tech, 7(1), 2013, 41-45. |
| [11] | S. Vidyalakshmi, T. R. Usharani, M. A. Gopalan, “Integral solutions of non-homogeneous ternary cubic equation ax2+by2=(a+b)z3”, Diophantus J. Math 2(1), 2013, 31-38. |
| [12] | S. Vidhyalakshmi, M. A. Gopalan, S. Aarthy Thangam, “On the ternary cubic Diophantine equation 4(x2+x)+5(y2+2y)=-6+14z3” International Journal of Innovative Research and Review (JIRR), 2(3), July-Sep 2014, 34-39. |
| [13] | M. A. Gopalan, S. Vidhyalakshmi, G. Sumathi, “On the homogeneous cubic equation with four unknowns X3+Y3=14Z3-3W2(X+Y)”, Discovery, 2(4), 2012, 17-19. |
| [14] | M. A. Gopalan, S. Vidhyalakshmi, N. Thiruniraiselvi, “On homogeneous cubic equation with four unknowns (x+y+z)3=z(xy+31w2)”, Cayley J. Math, 2(2), 2013, 163-168. |
| [15] | M. A. Gopalan, S. Vidhyalakshmi, N. Thiruniraiselvi, “On homogeneous cubic equation with four unknowns x3+y3=21zw2”, Review of Information Engineering and Applications, 1(4), 2014, 93-101. |
| [16] | M. A. Gopalan, S. Vidhyalakshmi, E. Premalatha, C. Nithya, “On the cubic equation with four unknowns x3+y3=31(k2+3s2)zw2”, IJSIMR, 2(11), Nov-2014, 923-926. |
| [17] | G. Janaki, C. Saranya, “Integral solutions of the ternary cubic equation 3(x2+y2)-4xy+2(x+y+1)=972z3”, IRJET, 4(3), March 2017, 665-669. |
| [18] | S. Vidhyalakshmi, M. A. Gopalan, A. Kavitha, “Observation on homogeneous cubic equation with four unknowns X3+Y3=72nZW2”, IJMER, 3(3), May-June 2013, 1487-1492. |
| [19] | S. Vidhyalakshmi, T. Mahalakshmi and M. A. Gopalan, “A Search On The Integer Solutions of Cubic Diophantine Equation with Four Unknowns x2+y2+4(35z2-4-w2)=6xyz”, International Journal of Grid and Distributed Computing, 13(2021), 2, 2581-2584. |
APA Style
Thiruniraiselvi, N., Kumar, S., Gopalan, M. A. (2024). Non-Homogeneous Binary Cubic Equation a(x-y)3=8bxy. Pure and Applied Mathematics Journal, 13(2), 29-35. https://doi.org/10.11648/j.pamj.20241302.12
ACS Style
Thiruniraiselvi, N.; Kumar, S.; Gopalan, M. A. Non-Homogeneous Binary Cubic Equation a(x-y)3=8bxy. Pure Appl. Math. J. 2024, 13(2), 29-35. doi: 10.11648/j.pamj.20241302.12
AMA Style
Thiruniraiselvi N, Kumar S, Gopalan MA. Non-Homogeneous Binary Cubic Equation a(x-y)3=8bxy. Pure Appl Math J. 2024;13(2):29-35. doi: 10.11648/j.pamj.20241302.12
@article{10.11648/j.pamj.20241302.12,
author = {Nagarajan Thiruniraiselvi and Sharadha Kumar and Mayilrangam Ambravaneswaran Gopalan},
title = {Non-Homogeneous Binary Cubic Equation a(x-y)3=8bxy
},
journal = {Pure and Applied Mathematics Journal},
volume = {13},
number = {2},
pages = {29-35},
doi = {10.11648/j.pamj.20241302.12},
url = {https://doi.org/10.11648/j.pamj.20241302.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.pamj.20241302.12},
abstract = {Polynomial equations an interesting subject in theory of numbers, occupy a pivotal role in the realm of mathematics and have a wealth of historical significance. The theoretical importance of polynomial equations of third degree in two unknowns having integral coefficients is great as they are closely connected with many problems of number theory. Specifically, the third degree polynomial equations having two unknowns in connection with elliptic curves occupy a pivotal role in the region of mathematics. This paper discusses on finding many solutions in integers to a typical third degree equation having two variables expressed as a(x-y)3=8bxy. The substitution strategy is employed in obtaining successfully different choices of solutions in integers. Some of the special fascinating numbers, namely, Pyramidal numbers, Polygonal numbers, Centered pyramidal numbers, Centered polygonal numbers, Thabit ibn Qurra numbers, Star numbers, Mersenne numbers and Nasty numbers (numbers expressed as product of two numbers in two different ways such that the sum of the factors in one set equals to the difference of factors in another set) are discussed in properties. These special numbers are unique. and have attractive characterization that set them apart from other numbers. The process of formulating second order Ramanujan numbers with base numbers as real integers is illustrated through examples.
},
year = {2024}
}
TY - JOUR T1 - Non-Homogeneous Binary Cubic Equation a(x-y)3=8bxy AU - Nagarajan Thiruniraiselvi AU - Sharadha Kumar AU - Mayilrangam Ambravaneswaran Gopalan Y1 - 2024/06/19 PY - 2024 N1 - https://doi.org/10.11648/j.pamj.20241302.12 DO - 10.11648/j.pamj.20241302.12 T2 - Pure and Applied Mathematics Journal JF - Pure and Applied Mathematics Journal JO - Pure and Applied Mathematics Journal SP - 29 EP - 35 PB - Science Publishing Group SN - 2326-9812 UR - https://doi.org/10.11648/j.pamj.20241302.12 AB - Polynomial equations an interesting subject in theory of numbers, occupy a pivotal role in the realm of mathematics and have a wealth of historical significance. The theoretical importance of polynomial equations of third degree in two unknowns having integral coefficients is great as they are closely connected with many problems of number theory. Specifically, the third degree polynomial equations having two unknowns in connection with elliptic curves occupy a pivotal role in the region of mathematics. This paper discusses on finding many solutions in integers to a typical third degree equation having two variables expressed as a(x-y)3=8bxy. The substitution strategy is employed in obtaining successfully different choices of solutions in integers. Some of the special fascinating numbers, namely, Pyramidal numbers, Polygonal numbers, Centered pyramidal numbers, Centered polygonal numbers, Thabit ibn Qurra numbers, Star numbers, Mersenne numbers and Nasty numbers (numbers expressed as product of two numbers in two different ways such that the sum of the factors in one set equals to the difference of factors in another set) are discussed in properties. These special numbers are unique. and have attractive characterization that set them apart from other numbers. The process of formulating second order Ramanujan numbers with base numbers as real integers is illustrated through examples. VL - 13 IS - 2 ER -